Komplexní teoretické i praktické vysvětlení PageRanku

PageRank jako výchozí algoritmus hodnocení důležitosti vzájemně propojených stránek je základem úspěšnosti Googlu. Článek se zaměřuje na podrobné vysvětlení algoritmu a jak se vyvíjel v čase. Také obsahuje příklad výpočtu PageRanku pro skupinu propojených stránek.
Myslím, že není třeba na tomto místě popisovat, co je PageRank a kde se používá. Co ale už ne všichni znají, je jeho historie. PageRank vznikl jako výzkumný projekt Page a Brina při jejich postgraduálním studiu. Prvně byl prezentován v roce 1998 v pracích The Anatomy of a Large-Scale Hypertextual Web Search Engine a The PageRank Citation Ranking: Bringing Order to the Web. Tyto dva dokumenty jsou vedle patentů Googlu jediné dostupné zdroje informací od autorů PageRanku. Nutno ještě dodat, že PageRank není zdaleka jediný algoritmus pro řazení výsledků a hodnocení důležitosti stránek, které Google v současné době používá. Ale určitě je to zajímavý koncept, který pomohl dostat Google tam, kde dnes je. V následujících odstavcích bych rád popsal původní koncept PageRanku, jeho vývoj a možnosti jeho optimalizace pomocí Markovových řetězců, jak navrhují další autoři.
Originální definice podle Page
Jakákoli stránka má vysoké hodnocení, jestliže suma jejích hodnocení ze zpětných odkazů je vysoká. To pokrývá možnost získání vysokého hodnocení z mnoha zpětných odkazů, ale i druhý případ, kdy stránka má několik málo zpětných odkazů zato s vysokým hodnocením. Zpětným odkazem se rozumí odkaz z libovolné jiné stránky mířící na hodnocenou stránku.
Základní definice
Nechť Sj je webová stránka, BSj je skupina stránek které odkazují na Sj (zpětné odkazy) a | Si | značíme počet odchozích odkazů na stránce Si.
PageRank stránky Sj, označený jako pr(Sj) je suma všech PageRanků stránek směřující na Si, dělená počtem odchozích odkazů na stránce Si:

Rovnice 1
Připomeňme, že hodnocení stránky je rozděleno mezi její linky odkazující na jiné stránky, případně přispívají k hodnocení (jsou přičítána k hodnocení) odkazovaných stránek. Problém rovnice 1 tkví v hodnotě výchozího PageRanku pr(Sj), hodnota této funkce je neurčená. Brin a Page řeší tento problém rekurzivním výpočtem. Rovnice je tak spočitatelná, přiřadíme-li libovolné vstupní hodnoty pr(Si) a iterujeme výpočet, dokud hodnoty nezačnou konvergovat.
Na obrázku 1 je zobrazeno předání hodnocení ze dvou stránek na levé straně páru stránek vpravo. Hodnocení se z různých zdrojů sčítá a při předávání se dělí počtem odkazů, kterými se přenáší na další stránky.

Obrázek 1: Zjednodušený výpočet PageRanku
Problémové oblasti
Page a Brin již ve své původní práci upozorňují na problém zvaný rank sink (zabředlé hodnocení). Rank sink nastává v případě, kdy máme dvě stránky které odkazují pouze samy na sebe a ne na žádnou jinou webovou stránku. A představte si, že existuje stránka která na jednu z nich odkazuje, tzn. předává jí část svého PageRanku. V průběhu výpočtu PageRanku těchto stránek, jednotlivých iterací, tyto dvě stránky načítají hodnocení, ale žádné nepouštějí. Tato smyčka je jakási past. Aby vyřešili tento problém, zavádějí zdroj hodnocení, tj. výchozí hodnoty, kterou má každá stránka sama od sebe.

Obrázek 2: Příklad rank sink u S1 a S2
Další problémovou situací, na kterou narazili, jsou slepé odkazy (dangling links). Jedná se o odkazy, které míří na stránku, která nemá žádné odkazy (dangling site). Může se buď jednat o odkaz na URL, které neexistuje, nebo se z nějakého důvodu crawleru nepodařilo stránku načíst, nebo ji zatím ještě nestihl načíst. Další možnost je, že odkaz vede na obrázek, PDF, prostý text nebo prostě HTML stránku, která neobsahuje žádný odchozí odkaz.

Obrázek 3: Příklad dangling site (S5)
Původní řešení problémových situací
K vyřešení problémový oblastí zavedli Page a Brin model náhodného návštěvníka (random surfer). Jedná se o předpoklad uživatelského chování na webu, kdy tento návštěvník kliká po odkazech, nikdy nejde zpět, ale někdy se nudí a začne na jiné náhodné stránce (přeskočí). Pro tento účel zavádějí tlumící faktor d (damping factor). Proměnná d nabývá hodnot v intervalu 0 až 1 a značí, jaká je pravděpodobnost, že náhodný návštěvník bude pokračovat na dalším odkazu. Hodnota 1 – d naopak vyjadřuje pravděpodobnost, že začne na nové náhodné stránce. Proměnná d je obvykle číslo okolo 0,85 (viz The Anatomy of a Large-Scale Hypertextual Web Search Engine).
Změněnou rovnice dle této úpravy můžeme zapsat výpočet PageRanku následovně:

Rovnice 2
Původní maticové vyjádření
Page a Brin zmiňují možnost vyjádření PageRanku pomocí matic. Definují matici A jako čtvercovou matici s řádky a sloupci korespondující s webovými stránkami. Jestliže existuje odkaz z i do j nechť Ai,j = 1/|Si| jinak položme Mi,j = 0. Další popis maticového vyjádření je poměrně stručný bez podrobného vysvětlení. Bohužel originální text si nedovolím zde reprodukovat a odkazuji přímo na The PageRank Citation Ranking: Bringing Order to the Web. Nevím jestli je to pouze mé laické nepochopení, nebo záměr autora, aby obsah byl těžko pochopitelný a algoritmus přesně reprodukovatelný.
Komplexní popis maticového vyjádření PageRanku za pomoci Markovových řetězů naleznete níže.
Úpravy PageRanku
Korekce damping faktoru
Rovnice 2 tak, jak byla zapsána v původním dokumentu, obsahuje drobnou nepřesnost. Dle The Anatomy of a Large-Scale Hypertextual Web Search Engine musí být suma všech PageRanků v celém indexu rovna jedné. Z tohoto důvodu by správně měla rovnice 2 vypadat následovně:

Rovnice 3
kde n je počet všech hodnocených stránek. Tzn. damping faktor, který značí pravděpodobnost, že náhodný návštěvník přijde na tuto stránku přímo 1-d (přeskočí, nedostane se z žádného odkazu), je dělen počtem všech stránek v daném souboru.
Iterační zápis
První spíše korekturní úpravou je zanesení iteračního procesu do rovnice 3. Langville v knize Google’s PageRank and Beyond: The Science of Search Engine Rankings navrhuje změnu rovnice následovně:
Nechť prx+1 (Sj) je PageRank stránky Sj při x + 1 iteraci, pak:
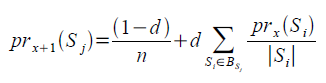
Rovnice 4
Iterační proces je inicializován při pr(Sj) = 1/n (kde n je počet všech stránek ve zkoumaném souboru) pro všechny stránky Sj a je opakován až do chvíle, kdy PageRank bude konvergovat ke stabilním hodnotám. Prvotní nastavení prk(Sj) = 1/n vlastně znamená, že všechny stránky v daném souboru začínají se stejným PageRankem v hodnotě 1/n.
Maticový zápis
Původní rovnice 1 resp. rovnice 3 počítají PageRank vždy jen pro jednu stránku. Použitím maticového zápisu lze počítat PageRank pro celý soubor stránek. To dává předpoklad k algoritmicky jednoduššímu výpočtu, který je rychlejší, méně náročný na výpočetní zdroje, což je v realitě miliard stránek výrazný faktor.
Budeme uvažovat PageRank jako jednoduchý vektor PR = 1 x n, který obsahuje hodnocení všech stránek v daném souboru. Definujeme matici odkazů L, čtvercovou matici n x n následovně:

Rovnice 5
kde o(Si,Sj) značí odkaz ze stránky Si na stránku Sj. Jestliže existuje odkaz ze stránky Si na stránku Sj, pak o(Si,Sj) = 1/|Si|, jinak o(Si,Sj) = 0. Součet všech hodnot na každém řádku se musí rovnat jedné, tzn. součet poměru předávaného hodnocení z každé stránky je 1. To ale neplatí o dangling stránkách, které neobsahují žádný odkaz. Proto zavedeme poslední úpravu výpočtu PageRanku. V případě, že se jedná o dangling stránku, tzn. v matici L, jsou na daném řádku samé nuly, v matici T nahradíme tyto nuly 1/n .
Dostáváme tak upravenou matici T:

Rovnice 6
Jestliže Si neobsahuje žádný odkaz (dangling stránka), pak ai = 1 jinak ai = 0. Tato matice T má vlastnost potřebnou pro aplikaci teorie Markovových řetězců, a to že je stochastická.
Výpočet PageRanku můžeme zapsat následovně:

Rovnice 7
Je zajímavé, že Brin a Page ve svých původních pracích vůbec nezmínili Markovovy řetězce, i když jejich navržené úpravy jsou právě jejich aplikací. Teorie Markovových řetězců je známá již od roku 1906 a od té doby dobře rozpracovaná. Mnoho autorů za pomocí této teorie zkoumá další zlepšení PageRanku, ať už z hlediska algoritmické efektivnosti s cílem rychlejšího výpočtu, tak z hlediska kvalitativního rozšíření.
Markovův řetězec
Pojmem Markovův řetězec označujeme stochastický proces, který má Markovovskou vlastnost. Ta říká, že v každém stavu procesu je pravděpodobnost navštívení dalších stavů nezávislá na dříve navštívených stavech. To znamená, že chování v Markovových řetězcích je „bezpaměťové“. V každém konkrétním stavu je možno zapomenout historii, tj. posloupnost stavů předcházející stavu současnému. Markovovy řetězce dostaly jméno po matematiku Andreji Markovovi.
Markovův řetězec si lze představit jako orientovaný graf, kde každé hraně je přiřazena její fixní pravděpodobnost tak, aby součet pravděpodobností všech hran vycházejících z daného uzlu byl roven jedné.
Implementací Markovova řetězce je právě PageRank. Strukturu webových stránek lze modelovat pomocí Markovova řetězce, kde jednotlivé stránky jsou zobrazeny jako uzly a hrany odpovídají odkazům mezi nimi.
Komplexní příklad
Na následujícím příkladu je ukázáno několik případů vzájemného propojení webových stránek. Stránky S1 a S2 jsou příkladem zabředlého hodnocení – rank sing.

Obrázek 4: Komplexní příklad
PageRank se předává ze stránky S3 na stránku S2 a zde už se předává cyklicky z S2 > S1 > S2 a tak dále. S5 je příklad dangling links. Tato stránka neobsahuje žádné odchozí odkazy a pouze PageRank přijímá ze zpětných odkazů ze stránek S3 a S4. Stránka S3 je také specifická, protože hodnocení pouze předává, ale žádné nezískává. V následujícím příkladu vypočteme konkrétní hodnoty PageRanku pro tyto stránky, což je zajímavé pro představu fungování hodnocení i v takovýchto krajních případech. Budeme postupovat podle výše definovaných rovnic, a to jak iteračním, tak maticovým výpočtem.
Iterační výpočet příkladu
Budeme vycházet z upravené iterační rovnice 4:
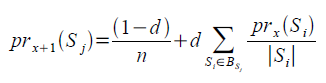
Nastavíme damping faktor na d = 0,85. Nultou iteraci začneme s pr(Sj) = 1/n, tzn. 1/5. Vypočteme PageRank pro každou stránku S z našeho příkladu.

Z této tabulky je zřejmé, že výpočet PageRanku pomocí rovnice 4 nedává součet všech hodnocení stránek v daném souboru roven jedné. Tato chyba je zapříčiněná nedokonalostí rovnice 4, která nepočítá s problémem dangling stránek, tedy stránek neobsahující žádný odkaz. V našem příkladu se jedná o stránku S5 , která hodnocení přijímá od S4 a S3, ale žádné již nepředává. V každé iteraci se tak ze systému toto hodnocení vytrácí. Tento problém řeší konkrétně definice (rovnice 6), resp. celkový výpočet PageRanku pomocí rovnice 7, viz dále.
Maticový výpočet příkladu
Do rovnice 6 dosadíme do řádků poměr hodnocení na stránce Si, které předává stránce Sj v daném sloupci.
Tzn. Si j = 1 / | Si |, jestliže vede odkaz z Si stránku Sj, v opačném případě zapíšeme nulu. V případě stránky S5, která neobsahuje žádný odkaz, uvažujeme, že náhodný návštěvník dál skočí na libovolnou stránku v souboru. Stránka S5 jako by obsahovala odkazy na všechny stránky. Dostáváme matici T, kde součty všech řádků se rovnají jedné.
Maticový výpočet příkladu
Do rovnice 6 dosadíme do řádků poměr hodnocení na stránce Si, které předává stránce Sj v daném sloupci.
Tzn. Si j = 1 / | Si |, jestliže vede odkaz z Si stránku Sj, v opačném případě zapíšeme nulu. V případě stránky S5, která neobsahuje žádný odkaz, uvažujeme, že náhodný návštěvník dál skočí na libovolnou stránku v souboru. Stránka S5 jako by obsahovala odkazy na všechny stránky. Dostáváme matici T, kde součty všech řádků se rovnají jedné.

Tuto matici dosadíme do rovnice 7. Vektor PR jsme získali jako součet sloupců matice v nulté iteraci.
Kolem 26. iterace hodnoty PageRanku začínají konvergovat a dvě desetinná místa jsou dále neměnná.
Suma PageRanků je v tomto příkladě rovna pěti (drobná nepřesnost je zapříčiněná zaokrouhledním). Abychom dostali hodnotu reálných PageRanků, musíme ji vydělit počtem stránek v souboru.
PR = (0,390 0,406 0,065 0,046 0,093) V tomto souboru stránek máme 39% šanci, že se náhodný návštěvník dostane na stránku S1, 40,6 % na stránku S2, 6,5 % času při procházení stráví na S3, nejméně bude navštěvovat S4 v 4,6 %, a stránku S1 navštíví v 9,3 % času.
Závěr
Věřím, že tento článek pomohl lépe pochopit základní algoritmus, na kterém Google vznikl: PageRank jako citační analýza na webu. Možná se mnou budete nesouhlasit, ale podle mě byly PageRank, schopnost škálovatelnosti technické platformy a výborné PR tři základní faktory, bez kterých by se Google k IPO nedostal. Přidejme k tomu schopnost nenásilně monetizovat návštěvníky pomocí kontextové reklamy, což můžeme přičíst jak dobrým akvizicím Applied Semantics a Sprinks tak i vlastnímu vývoji. A dostanete společnost s tržbami téměř 22 miliard USD za rok 2008, kde 97 % pochází z reklamy a 66 % reklamy na jejich serverech (drtivá většina Adwords z hledání).





Děkuji za vynikající článek. Mám jednu poznámku (spíše dotaz). Co
stránka, která odkazuje sama na sebe? Kdyby na obrázku 4 měla S4 několik
odkazů sama na sebe (například 3). Trochu by to algoritmus zmátlo. V matici
T by 4 řádek byl 0 0 0.2 0.6 0.2 a algoritmus by pak mohl dát
„pokřivené“ výsledky. Obecně vysoká (spíše jakákoliv nenulová)
čísla na hlavní diagonále matice by byly problém. Sám nevím jak se tohle
řeší. Jednoduché řešení, které se nabízí, je ignorovat odkazy na sebe
sama. To znamená na hlavní diagonálu dát vždy nuly. Tohle je ale v rozporu
s pravidlem, že pokud ze stránky nevede žádný odkaz, je hodnota
předávaného PR dána jako 1/n (jak se píše v článku). Jinýmy slovy
problém je v prvku matice T na pozici 5,5. Což znamená, že stránka,
která neodkazuje nikam zvýší sama sobě PR, ale stránka, která odkazuje
jen sama na sebe by nezvýšila nic. Možná na hlavní diagonále jsou vždy
nuly a pokud ze stránky nevede odkaz, tak předává ostatním (kromě sebe) ne
1/n jak se píše v článku, ale 1/(n-1). V praxi je číslo n tak vysoké,
že je úplně jedno, jestli je někde 1/n, nebo 1/(n-1). Takže to asi ani
nikdo neřeší.
Dobrý den Radime,
děkuji za pochvalu. Bohužel tento příklad se v originální literatuře
neřeší a spíše je v oblasti spekulací (např. http://www.webmasterworld.com/…30/31315.htm,
http://www.webworkshop.net/pagerank.html).
Osobně se přikláním k Vašemu názoru. Tzn. odkazy, které vedou na sebe
sama jsou prostě ignorovány a nezapočítávají se jak do počtu odchozích
odkazů (kterými se dělí předávaný pagerank) tak do příchozích odkazů
na danou stránku.
Problematiku sice sleduji jen okrajově, ale přesto mě velice zaujal
postupný vývoj rovnic a vůbec myšlenkové postupy okolo PR.
Jenom je škoda, že Google nezveřejní svůj aktuální algoritmus,
určitě by bylo zajímavé sledovat, jak jej vyvíjeli dál :)
Kdyby ho Google zverejnil, tak spousta lidi prijde na to, jak ho oblbnout a
jejich vyhledavac ztrati smysl.
Je to asi podobne, jako kdyz zverejnis spamfiltr, tak neni problem vyrobit
spam, ktery tim filtrem projde.
Pokud někoho zajímá, jaké jsou weby s nejvyšším Pagerankem v ČR
doporučuji mrknout na http://katalog.czin.eu/top-pr-100/ –
kde je komplexní přehled…
Tyhle katalogy jsou hrozne vyhodne. Nekdo si da vas odkaz na stranku ktera se
generuje dynamicky, a tim je vlastne na vsech strankach odkaz. a vy mu dáte
jeden odkaz. To potom PR roste ;-).
Ten seznam je o ničem :-(, zobrazuje pouze stránky vedené v nějakém
katalogu
Děkuji za tento článek, je psaný pochopitelnou formou a hezky postupně.
Takových jen více!
Ke kompletnímu prostudování článku jsem se dostal až teď, ale
dodatečně Vám musím poděkovat za vynikající vysvětlení PageRanku.
Jen malinkatá poznámka: Vysvětlení Markovova řetězce bych posunul
výše. V článku je zmíněn několikrát ještě před tímto rámečkem a
než jsem se k němu dostal, našel jsem si ho na Wikipedii.
Nicméně i tak vysoce kvalitní práce!